Navigation :EXPO21XX>愿景21xx>H15：研究与大学> Royal Holloway, University of London
Royal Holloway, University of London
  • Offer Profile
  • MR是一组工具，该工具实现了用于处理1D信号，2D图像和3D数据量的多尺度方法。

    MR多分析分析软件提供的内容
    • Scale and Resolution
    • Image and Data Analysis
    • Extensive Signal and Noise Modeling
    • 创新和性能
    • Financial Modelling, Nowcasting, Prediction
    • Wavelet and multiresolution transforms, ridgelet and curvelet transforms
产品介绍

  • Description

  • MR是由CEA（法国Saclay）和Nice Observatory开发的一组软件组件。该项目起源于天文学，涉及围绕多尺度分析构建的一系列创新方法的发展。MR软件组件几乎包括书籍图像和数据分析中介绍的所有应用程序：多尺度方法。这些应用程序的描述也可以在许多发表的论文中找到。MR的目标是不替换现有的图像处理软件包，而是要补充它们，为用户提供一组完整的多分辨率工具。这些工具是可执行的程序，它们在广泛的平台上工作，与当前的图像处理系统无关。它们允许用户使用多分辨率执行各种任务，例如小波变换，过滤，反卷积等。程序也可以从Java接口调用。软件包中包含了一组IDL（研究系统公司的交互式数据语言）和PV-WAVE（Visual Numerics Inc.）例程。将可执行文件连接到这些图像处理软件包。MR是一个重要的软件包，向其他领域的物理，空间和医疗领域的科学家介绍了前线方法。 to engineers in such disciplines as geology and electrical engineering; and to financial engineers and those in other fields requiring control and analysis of large quantities of noisy data.

    近年来已经开发了小波和其他多分辨率技术，并提供了对数据的强大而有见地的表示。通过多解决或多尺度分析，可以将图像分解为一组图像（或尺度），每个刻度仅包含给定尺寸的结构。与噪声建模相关联的该数据表示已应用于非常不同的应用程序，例如数据过滤，反卷积，压缩，对象检测等。结果在所有此类处理中都得到了增强，因为小波变换方法可以更好地理解图像中数据值的分布方式以及如何与噪声分开的信号。该项目的目的是开发使用多尺度批准的新方法来处理数据处理。已经实现了几种MR/1，MR/2，MR/3和MR/4的产品。

  • MR/1: Multiresolution and Applications

  • MR/1 is a set of software components developed by CEA (Saclay, France) and Nice Observatory. This project originated in astronomy, and involved the development of a range of innovative methods built around multiscale analysis. The MR/1 software components include almost all applications presented in the book Image and Data Analysis: the Multiscale Approach . Descriptions of these applications can also be found in many published papers . The goal of MR/1 is not to replace existing image processing packages, but to complement them, offering the user a complete set of multiresolution tools. These tools are executable programs, which work on a wide range of platforms, independently of current image processing systems. They allow the user to perform various tasks using multiresolution, such as wavelet transforms, filtering, deconvolution, and so on. Programs can also be called from a JAVA interface. A set of IDL (Interactive Data Language, by Research Systems Inc.) and PV-Wave (Visual Numerics Inc.) routines are included in the package which interface the executables to these image processing packages. MR/1 is an important package, introducing front-line methods to scientists in the physical, space and medical domains among other fields; to engineers in such disciplines as geology and electrical engineering; and to financial engineers and those in other fields requiring control and analysis of large quantities of noisy data.

    小波和多尺度变换
    Many 1D and 2D wavelet transforms and other multiscale methods, such the Pyramidal Median Transform or the lifting scheme, have been inplemented in MR/1.

  • 噪声建模：

    • Our noise modeling in the wavelet space is based on the assumption that the noise in the data follows a distribution law, which can be:
    • 高斯分布
    • 泊松分布
    • 泊松 +高斯分布（CCD检测器中的噪声）
    • Poisson noise with few events (galaxy counts, X-ray images, point patterns)
    • 斑点噪音
    • Correlated noise
    • 均方根地图：我们具有每个数据值的噪声标准偏差。
    如果噪声不遵循这些分布中的任何一个，我们可以从以下任何假设中得出噪声模型
    • 它是静止的，我们有一个子图像，其中包含噪声的实现，
    • it is additive, and non-stationary,
    • 它是乘法和固定的，
    • it is multiplicative, but non-stationary,
    • it is undefined but stationary,
    • it is additive, stationary, and correlated.

  • 应用程序:

  • 1. Descriptions of these applications can also be found in many published papers .
    2.General tools: data conversion, simulation, statistic, Fourier analysis, mathematical morphology, principal component analysis, ...
    3. 1d和2d小波变换和重建..数量对象操纵：统计，频段提取，比较，...
    4. Multiresolution support detection.
    5. 1D and 2D filtering taking into account the different noise models. Many methods have been implemented (11 in 1D and 18 in 2D) including standards like K
    Sigma thresholding, SURE, MAD, Universal thresholding, Multiscale Wiener filtering, ...
    6. Image background subtraction.
    7. Image deconvolution: nine standard deconvolution methods are available (MEM, LUCY, Landweber, MAP, ...), and five wavelet based methods.
    8.图像注册。
    9. Lossy and lossless image compression. the PMT (median based compression method) and the bi-orthogonal wavelet transform allows both the user to
    reconstruct an image (or a part of an image) at a given resolution. Lossless image compression is based on the lifting scheme.
    10.使用多尺度视觉模型在1D和2D数据集中进行对象检测和提取。
    11. Edge detection and image reconstruction from the multiscale edges. Many standard edge detection methods are available (15) and two wavelet based methods.
    12. Contrast enhancement. Standard methods and contrast enhancement methods based on the wavelet transform are available.
    13. 1D Wavelet Transform Modulus Maxima (WTMM) representation and reconstruction.
    14. 1D Multifractal analysis.
    15. Time-Frequency analysis (Short Term Fourier Transform, Wigner-Ville transform).
    16.时间序列的现代和预测。

  • MR/2: Multiscale Entropy and Applications

  • “熵”是由于克劳修斯(1865),和the concept of entropy was introduced by Boltzmann into statistical mechanics, in order to measure the number of microscopic ways that a given macroscopic state can be realized. Shannon (1948) founded the mathematical theory of communication when he suggested that the information gained in a measurement depends on the number of possible outcomes out of which one is realized. Shannon also suggested that the entropy can be used for maximization of the bits transferred under a quality constraint. Jaynes (1957) proposed to use the entropy measure for radio interferometric image deconvolution, in order to select between a set of possible solutions that which contains the minimum of information, or following his entropy definition, that which has maximum entropy. In principle, the solution verifying such a condition should be the most reliable. Much work has been carried out in the last 30 years on the use of entropy for the general problem of data filtering and deconvolution. Traditionally information and entropy are determined from events and the probability of their occurrence. Signal and noise are basic building-blocks of signal and data analysis in the physical and communication sciences. Instead of the probability of an event, we are led to consider the probabilities of our data being either signal or noise. Consider any data signal with interpretative value. Now consider a uniform "scrambling" of the same data signal. (Starck et al., 1998, illustrate this with the widely-used Lena test image.) Any traditional definition of entropy, the main idea of which is to establish a relation between the received information and the probability of the observed event, would give the same entropy for these two cases. A good definition of entropy should instead satisfy the following criteria:
    • 1.平面信号中的信息为零。
    • 2.信号中的信息量与背景无关。
    • 3.信息量取决于噪声。如果噪声高或小，给定的信号y（y = x +噪声）无法提供相同的信息。
    • 4.熵必须以相同的方式工作，以使具有B + epsilon的信号值（B为背景），并且具有值B -Epsilon的信号值。
    • 5.信息量取决于信号中的相关性。如果信号s在噪声上方显示大型功能，则包含大量信息。通过从s中生成一组新的数据，通过随机获取S中的值，大型功能显然会消失，并且该新信号将包含更少的信息。但是数据值将与S相同。
    为了迎合背景，我们将多解析的概念介绍给我们的熵。我们将考虑一些数据集中包含的信息是不同分辨率级别的信息的总和。小波变换是我们数据的多尺度分解的一种选择。我们定义位置k和j处的小波系数WJ（k）的信息，为i = -ln（p（wj（k））），其中p是小波系数的概率。然后，通常表示为H的熵被定义为所有位置的总和在所有位置上的总和j，j，j in j in j as l l i. j，对于高斯噪声，我们使用高斯概率分布继续朝这个方向沿着这个方向继续，发现熵，熵，h，是所有位置k的总和（wj（k）^2）/（2 sigma^2 j）（即系数平方，除以两倍的标准偏差平方，给定比例）。Sigma或标准偏差是噪声的（高斯）度量。我们看到该信息与小波系数的能量成正比。小波系数越高，那么概率就越低，并且该小波系数提供的信息越高。 Our entropy definition is completely dependent on the noise modeling. If we consider a signal S, and we assume that the noise is Gaussian, with a standard deviation equal to sigma, we won't measure the same information compared to the case when we consider that the noise has another standard deviation value, or if the noise follows another distribution. Returning to our example of a signal of substantive value, and a scrambled version of this, we can plot an information versus scale curve (e.g. log(entropy) at each scale using the above definition, versus the multiresolution scale). For the scrambled signal, the curve is flat. For the original signal, it increases with scale. We can use such an entropy versus scale plot to investigate differences between encrypted and unencrypted signals, to study typical versus atypical cases, and to differentiate between atypical or interesting signals.

  • MR/3：3D和多通道数据

  • MR/3 deals with the analysis of multi-channel data or 3D data.
    3D data can either be a real cube, or a set of images of the same observation, but taken at different times. Multi-channel data can be either 1D or 2D multi-channel:
    • 1D多通道：在几个波长或不同时间观察到1D信号。结果是图像。
    • 2D multi-channel: a 2D signal (image) is observed at several wavelengths or at different times. The result is a cube. A special case of multi-channel images is color images. In this case, we have three channels. Several color coordinate systems exist. The most widely-used is the RGB system. Each pixel is identified by three values R, G, and B corresponding to the three colors red, green, and blue. Applications in MR/3 are

      1.一般工具：统计，操作，噪声模拟，转换...
      2.多维数据集和小波transform

        1. 3D圆柱小波变换和重建。
        2. 3D双向波波转换和重建。
        3. 3D小波转换操作（带提取，...）。
        4. 3D data filtering using the wavelet transform.
      3. Multi-channel Data
        1. 1D和2D小波Karhunen-Loeve变换（WT-KLT）和重建。
        使用WT-KLT 2、1D和2D多通道数据过滤。
        3.独立的组件分析。
      4.Color images
        1 .RGB image compression.
        2. RGB图像过滤。
        3. RGB image contrast enhancement.
      5.多时间图像
        1. Images coaddition taking into account vertical and horizontal shifts.
        2.图像对垂直和水平偏移的反卷积。

  • MR/4: Ridgelet and Curvelet

  • MR/4deals with the ridgelet and the curvelet transforms.
    当数据呈现各向异性特征时，小波会提出一些局限性。新方法，例如Ridgelet变换和CURVELET变换，可以更好地适应此类数据。也可以组合小波，山脊和旋转仪，以使每个人的优势受益。
    MR/4中的申请是

    General tools: statistic, operations, noise simulation, conversion ....
    1. 2D Ridgelet：
      1. Ridgelet transform and reconstruction of images.
      2.统计数据相对于Ridgelet系数。
      3图像岭滤波器过滤。

    2. 2D CURVELET：

      1.图像的晶状体变换和重建。
      2.统计数据相对于路缘系数。
      3.孔值过滤。
      4. CURVELET变换的对比度增强。

    3. Color images and Curvelets:

      1. RGB图像对比度通过CURVELET变换增强。
      2. RGB图像CURVELET过滤。

    4. Combined Filtering Method.

  • 稀疏图像和信号处理

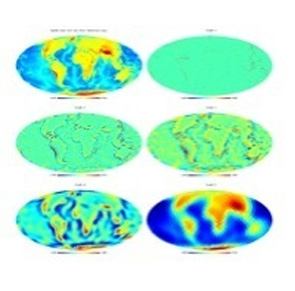
    • Pyramidal Wavelet Transform on the Sphere

    • The global relief data are ETOPO5 land and sea-floor elevation data. The isotropic pyramidal wavelet transform preserves detail, and is efficient in storage and computation. Chapter 10 discusses many aspects of multiscale geometric analysis on the sphere.

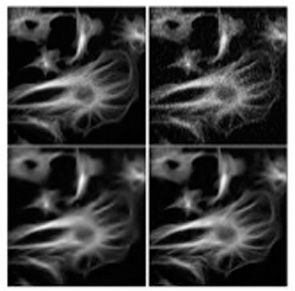
    • 过滤生物医学显微镜图像

    • 图像（左上）为荧光微管蛋白丝。右上方是一个嘈杂的版本，带有泊松噪音。较低的图像被过滤，如第6章所述，此噪声过滤是基于孔值转换来保存淡淡的特征。

    • Signal Recovery from Compressed Sampling

    • 压缩传感同时样品并压缩信号。Piet Mondrian绘画的图像是第11章中使用的一个示例，用于显示压缩感应如何处理大量图像数据的采集和传输。